[项目] 数据挖掘——Wine Data Set
Zoey Young 我的项目 Servlet 数据挖掘

数据源

来源

数据源的完整名称是Wine Data Set，是对3种不同的酒进行分类。这三种酒包括13种不同的属性，分别为：Alcohol, Malic acid, Ash, Alcalinity of ash, Magnesium, Total phenols, Flavanoids, Nonflavanoid phenols, Proanthocyanins, Color intensity, Hue, OD280/OD315 of diluted wines, Proline. 在“wine.data”文件中, 每行代表一种酒的样本, 共有178个样本; 一共有14列, 其中, 第一列为类标志属性, 共有三类, 分别记为“1”, “2”, “3”; 后面的13列为每个样本的对应属性的样本值. 其中第1类有59个样本，第2类有71个样本，第3类有48个样本。

算法介绍

本实验采用了两种算法对数据源进行分类，分别为朴素贝叶斯算法和K最近邻算法.

朴素贝叶斯分类算法简介

统计学的方法, 可以预测类成员关系的可能性, 即给定样本属于一个特定类的概率.

1、贝叶斯定理

后验概率(posteriori probabilities): P(H|X)表示条件X下H的概率.

贝叶斯定理:P(H|X)=P(X|H)P(H)/P(X)

2、朴素贝叶斯分类

每个数据样本用一个n维特征向量X={x1,x2,…,xn}表示，分别描述对n个属性A1,A2,..,An样本的n个度量.

假定有m个类C1,…,Cm,对于数据样本X,分类法将预测X属于类Ci,当且仅当

P(Ci|X) > P(Cj|X), 1 <= j <= m, j不等于i

根据贝叶斯定理, P(Ci|X)=P(X|Ci)P(Ci)/P(X)

由于P(X)对于所有类都是常数, 只需最大化P(X|Ci)P(Ci)

计算P(X|Ci), 朴素贝叶斯分类假设类条件独立. 即给定样本属性值相互条件独立. （在一般情况下此假定都能成立）

P(X|Ci)=P(X1|Ci)*P(X2|Ci)*...*P(Xn|Ci)

贝叶斯数据预处理

根据对所有属性数据的观察，采取了相对简单的预处理方法。代码如下：

public List<List<Integer>> discretization(List<List<Double>> data) {
    List<Double[]> minmax =  new ArrayList<Double[]>();
    minmax = getMinMax(data);
    List<List<Integer>> result =  new ArrayList<List<Integer>>();
    for (int i = 0; i < dimension; i++) {
        if (minmax.get(i)[0] > 100 && minmax.get(i)[1] > 1000) { // 如果最小值大于100且最大值大于1000，则所有值除以100
            for ( int j = 0; j < data.size(); j++) {
                data.get(j).set(i, data.get(j).get(i) / 100);
            }
        } else if (minmax.get(i)[0] > 10 && minmax.get(i)[1] > 100) { // 如果最小值大于10且最大值大于100，则所有值除以10
            for ( int j = 0; j < data.size(); j++) {
                data.get(j).set(i, data.get(j).get(i) / 10);
            }
        }
    }
    // 对所有值取整
    for ( int j = 0; j < data.size(); j++) {
        List<Integer> list =  new ArrayList<Integer>();
        for ( int i = 0; i < dimension; i++) {
            list.add(Arith.convertsToInt(data.get(j).get(i)));
        }
        result.add(list);
    }
    return result;
}

结果展示

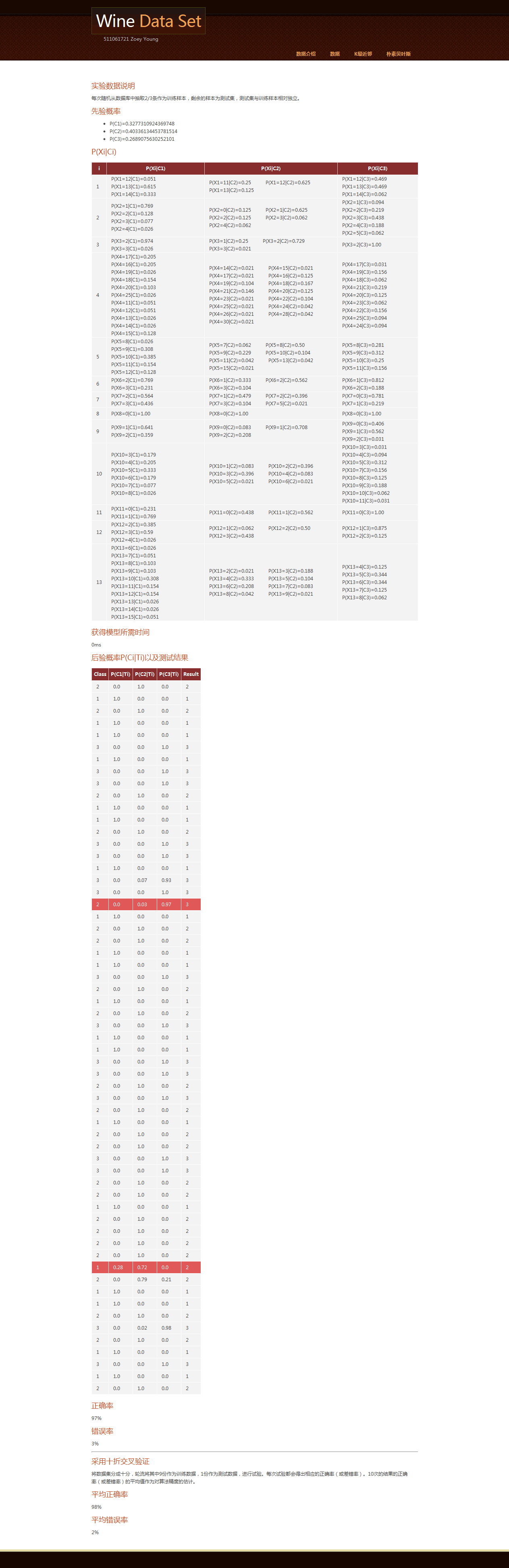
朴素贝叶斯

KNN算法简介

基于类比学习，通过比较训练元组和测试元组的相似度来学习。

将训练元组和测试元组看作是n维（若元组有n的属性）空间内的点，给定一条测试元组，搜索n维空间，找出与测试元组最相近的k个点（即训练元组），最后取这k个点中的多数类作为测试元组的类别。

KNN数据预处理

采用最小-最大规范化，将数据区间规范为[0,1]，对任意一个在原来区间中的变量，在新的区间中都有一个值和它对应，这是一个线性变换过程。

x'=(x-old_min)/(old_max-old_min)

代码如下：

public void minMaxDataFormat(List<List<Double>> data) {
    List<Double[]> minmax =  new ArrayList<Double[]>();
    minmax = getMinMax(data);
    for ( int i = 0; i < data.size(); i++) {
        for ( int j = 1; j < dimension; j++) {
            data.get(i).set(
                j,
                (data.get(i).get(j) - minmax.get(j)[0])
                / (minmax.get(j)[1] - minmax.get(j)[0]));
        }
    }
}

结果展示

KNN

项目结构

项目结构

算法的实现在KNN.java与NaiveBayes.java中。

Data.java用来获取数据并含有对数据进行预处理的算法。

ModelAssessment用来保存模型评估相关数据，暂时只保存正确率、错误率与算法执行时间。其它包中文件为数据库与Servlet相关。

源代码